An Exploration of Classification Models using Mobile Dataset

I wanted to review some classification algorithms, so I found a clean data set on Kaggle about classifying mobile price ranges to practice with logistic regression, decision tree algorithm, and random forest. I will be walking through my thought process when attempting this exploration of the data set from Kaggle.

The Dataset

The data set has its own story about how Bob wants to start his own mobile company, but does not know how to estimate the price of mobiles his company creates. He decides to collect sales data of mobile phones from various companies and decides to find some relation between the features of the phone and its selling price.

The features of the phone include battery power, bluetooth capabilities, clock speed, dual sim option, front camera mega pixels, 4G capabilities, internal memory, mobile depth, mobile weight, number of core processors, primary camera mega pixels, pixel height resolution, pixel width resolution, RAM, screen height, screen width, talk time with a single battery charge, 3G capabilities, touch screen, and wifi capabilities.

The data set has a test and train file, but because there were no price ranges in the test file, I decided to just use my training data and create a separate test file out of some of my training data. This decreased the amount of data I could train, but I felt that it was ok for this exploration.

Exploratory Data Analysis

Some things I did before I ran any models was to look at pairplots using seaborn. Since there were so many features, I separated the dataset into three groups with about 7-8 features in each set of pairplots and compared them with the price range, which is denoted  0, 1, 2, or 3. I looked at pairplots to see if there are any features that are linearly separable. (This would show me that I could use logistic regression and it would work well.)

How can I tell if some features are linearly separable or not? Well, I looked at each pairplot to see if there were features that overlapped the least. For example, if I look at the distribution plot of battery power with the different price ranges as the "hue" attribute, I see that the blue and red hues are clearly separated. There is definitely overlap, but there is a huge separation between the blue and red distributions.

There is some separation in the pixel width feature too.

But the separation with the RAM is most significant.

So you might ask what are some examples of features that do not look separable? Well, I would say the front camera pixels feature is not linearly separable, since there seems to be an equal distribution of all the four colors in the same way. Look at the front camera pixels distribution-- the colors overlap almost perfectly.

So, now I know that certain features like RAM, battery power, and pixel width may be very telling of the price range of mobile phones, but something like the front camera pixels might not be very telling.

Are classes balanced?

Another thing to look at before doing any modeling is to check the class balance of the target. My target has four classes that tell me how expensive a mobile phone is-- class 0, 1, 2, and 3. Looking at a distribution plot of the price range, I see that it is uniform. This rarely happens in real life, but again, this is a clean Kaggle data set.

Balanced classes tell me that I would not need to do any over or undersampling or class weights or change the threshold of my classes after modeling.

Logistic Regression Model

I used sci-kit learn's modules to run my logistic regression model. I did two train, test, splits to divide my data set into a train-validate-test set of 60-20-20.  I also imported StandardScaler to standardize my features. I looked at many metrics, including F1, accuracy, precision, and recall. I also decided to look at a confusion matrix, to practice and make sure that I am getting the metrics right.

For my logistic regression model, I just decided to focus on the three features I found that looked more linearly separable than the rest of the features--battery_power, ram, and px_width. I standard scaled my features, then fit my model to my training set. I predicted using my validation set and used a classification report to see the precision, recall, F1, and accuracy scores. Using just three features, I got an accuracy of 82%, and an F1 score of predicting class 0 as .91 and class 3 as .93, class 1 as .68, and class 2 as .71. That's not bad.

Logistic Regression-Confusion Matrix

This part will cover how to calculate precision, recall, and accuracy using the confusion matrix. The confusion matrix basically tells me the actual vs. predicted values of my target. For example, in this confusion matrix, there are 95 cases of phones predicted as class 0 and were actually class 0.

So, what is accuracy in relation to the confusion matrix? Accuracy is the total number of true positives over the total number of cases. (An example of a true positive is a case that is predicted to be 0 and is actually 0.) In this case, it is the sum of the diagonal that goes from top left to bottom right over the sum of the numbers in the whole matrix- 325/328 which rounds to .82 (same number as reported above).

What is precision in relation to the confusion matrix? Precision is the total number of true positives over the sum of true positives and false positives (an example of a false positive is a case that is predicted to be 0 but is not 0.). We will have to look at precision class to class. In this case, the total number of true positives for class 0 is 95. The total number of false positives is 19. So, the precision is 95/114 which rounds to .83.

What is recall in relation to the confusion matrix? Recall is the total number of true positives over the sum of true positives and false negatives. (An example of a false negative is a case that is predicted to not be 0 but is actually 0.) In this case, the total number of true positives for class 0 is 95 and the number of false negatives is 0, so precision is 1.

What is F1 in relation to precision and recall? F1 is actually the harmonic mean of the precision and recall scores.

Decision Tree

Using sklearn's decision tree algorithm is simple. You instantiate the DecisionTreeClassifier and set a max depth for the tree. Then you fit your training set and then predict using your validation set. The decision tree performed poorly in comparison to the logistic regression algorithm, with an accuracy of .26. We can guess the classes of the mobile phones and do just as well as the decision tree classifier.

I want to make a note that instead of using just three features, I used all the features available to me when training and fitting my decision tree.

The F1 score for class 0 was .28, class 1 was .33, class 2 was .14, and class 3 was .27.

Random Forest

Similarly, random forest did not perform that well compared to logistic regression. I used 1000 estimators (basically individual decision trees) and a max depth of 2 in my random forest model. The random forest basically averages out many decision trees to give a more robust and accurate prediction, but in this case, the accuracy score turned out o be .24. The F1 score for class 0 was .28, class 1 was .31, class 2 was .12, and class 3 was .27.

However, what was interesting to see was the feature importances in my random forest model. The following feature importance graph shows the relative importance of each feature in determining the information gained from splitting at that feature. Here, ram, battery power, px_height, and px_width showed the information gain. This is consistent with the fact that I noticed that ram, battery power and px_width showed much linear separability from the pairplots done in the exploratory data analysis portion above.

Logistic Regression worked best

A reason why I think logistic regression worked best in this scenario is that there were features that were linearly separable. In cases where there was little linearly separability, random forest might have worked better.

A final note

Improvements could be made on my model with more investigation of how to obtain a F1 score of when predicting class 1 and class 2 mobiles. Perhaps running a logistic regression model on all with all of the features and lowering the C parameter (a regularization parameter, which I set to 1 which means no regularization was used) to make sure the model doesn't over-fit. That would be interesting to see.

2019 Year In Reflection

As 2019 ends, I find myself being very excited for all the things I will be doing in 2020. But, first, it is important to reflect on the past year, express my gratitudes, and learn from my mistakes.

I knew the first thing of 2019 I will be doing is going to be the end (perhaps) of my career in teaching. I left the a teaching position in the Bronx and decided to study for an actuarial exam (FM) full time. But, I always had the feeling that an actuarial career path was a wrong puzzle piece in the picture of my life. I still tried hard to see if that puzzle piece would fit though. But, I tried other puzzle pieces too through networking with people from different walks of life and starting to dabble in some data projects. I connected with a data scientist friend and he showed me the work he was doing for his company at the time-- SQL queries, A/B testing, coding with Python, influencing decisions using insights gathered from data. Is this the future...(my future?) I thought.

When I passed FM in April, I made another decision. I will not continue to take actuarial exams. Instead, I will pursue this data science thing full-time. Was I fickle? Do I get swept away with interesting ideas and new things too easily? In retrospect, it seems like I was simply following my instincts and my instincts told me that data science could be right for me. But, instincts doesn't really give you all the technical skills you need to be a leader in data science. Although I had already studied some Python and done some data projects on my own, I was lacking in everything a modern day data scientist needed.

Therefore, I joined Metis, a 12 week data science bootcamp to skill up. Really, it was the start of a career change and a new chapter in my life where I met new friends and learned the basics and the latest of machine learning and data science. Although I say that Metis was the start of a career change, I believe my mindset has already been set in the beginning that I will change my career with success.

9 months into 2019, I have left my teaching job, passed an actuarial exam, and graduated from a data science bootcamp. The next three months was spent in coffee shops, yoga studios, cross-fit boxes, libraries, networking events, at home, but I had one main goal. I was going to find my first full time position as a data scientist...or analyst.

I can say that I have been scouted by a company and although it is for an internship, I am really happy that a door opened up for me in data science.

I know that 2019 has been really focused on my career change. My career change, although scary, has been the one thing that remained constant throughout the year.

As for all the people who made this year possible, I would have to thank my parents, sister, boyfriend, and all my friends. I'm grateful for the life I had lived.

Coming into the new year, I think there is one thing among many things that I would like to work on. It is being aware. I want to be more aware of myself, body and mind, and of the filters I put in the world. I believe being aware has been an unconscious goal of mind and I am really happy that I became aware of this goal of mine this time around and am able to articulate it with words.

Thank you 2019.

Notes on Root Mean Squared Error and R^2

Linear Regression Metrics

Two popular linear regression metrics are the root mean squared error and R^2.

Say you have a data set and have plotted the line of best fit. How well does the line of best fit actually model the data set? Visually, if the data points are very close to the line of best fit, you can say that it is a pretty good model compared to data points that are scattered everywhere and not particularly hugging the line of best fit. But, there is a more rigorous way of telling whether your linear model is good or not.

SSE- Sum of Squared Errors 

The most straightforward way to see whether or not your model is a good fit compared to other models is to find the sum of the squared errors. This means you sum up all the squared values of the difference of the actual values and the predicted values. The lower the sum, the better the model.

MAE- Mean Absolute Error

Another way to compare models is to find the mean absolute error, which is just the average of the absolute values of the difference of the actual values and predicted values. Again, the lower the mean, the better the model. SSE is more sensitive to outliers (since we are squaring the values) than MAE is. But, MAE requires less refinement to be interpretable since the MAE returns the original units of the values. You would need to divide SSE by the total number of values and then take the square root of that for it to be more interpretable. Which leads us to...

Root Mean Squared Error

The root mean squared error is simply the square root of the SSE divided by the total number of values. This creates a more interpretable metric for how good our model is. Again, RSME, like SSE is more sensitive to outliers and would penalize them more than MAE.

R^2

R^2, or the coefficient of determination, is another metric you could use to see how good your model is. R^2 is usually between 0 and 1, but there are cases where R^2 can be negative. (That's really 'bad'.) The idea behind R^2 is to measure the target "variance explained" by the model. (How much variance of the target can be explained by the variance of the inputs?)

SST, or the sum of the squares total) is the target's intrinsic variance from its mean. It is given by the sum of the squares of the difference of the actual values and the mean of the actual values.

SSE/SST gives us the percent of the variance that remains once you've modeled the data. The sum of the squared errors over the sum of the squares total is the portion of the variance that the model cannot explain. However, we can subtract SSE/SST from 1 and get the portion of the variance that the model can explain.

1 - SSE/SST is the coefficient of determination, or R^2. "R^2 measures how good [your] regression fit is relative to a constant model that predicts the mean".

(Usually SSE is smaller than SST, assuming that our model does a little or much better than just predicting the mean all the time, so R^2 is between 0 and 1.)

Forest Fires in Brazil

Context

As a person who cares about environmental issues, coming across a data set about forest fires in Brazil on Kaggle was very exciting. The data set contains the number of forest fires in 23 states in each month over the span of years from 1998 to 2017 reported by the Brazilian government. I decided to analyze the data set to find the trend of the number of forest fires, to find when forest fires occur with the highest frequency, and to create a Tableau dashboard to visualize the change in the number of forest fires over time.

engine = 'python'

When reading the csv file with the data set, I had to set the engine parameter to python because UTF-8 couldn't decode some characters.
I realized that the month names were in Portuguese, so I decided to change all the month names to numeric names. I created a new column in my dataframe that are the numeric equivalents to the month names.

Geocoding

 I wanted to have the latitude and longitude for each state in the data set so that I can graph it in the future. So, I used locationiq's API to find the latitude and longitude for each state.

I then was able to create a dictionary of the states and their respective latitude and longitude values. I was able to use two apply functions to apply to each row the correct latitude and longitude based on the state.

Average Number of Forest Fires Per Year in Each State

The visual I wanted to create is one of a map which shows the average number of forest fires per year in each state in the data set with a circle. The larger and darker the circle, the higher the average number of forest fires per year. I would need to create a dataframe with the average number of forest fires per year in each state first. Here is the code, which required use of a groupby:


Total Number of Forest Fires Per Year

It would be great if I could see the overall trend of forest fires throughout the years. I decided to use another groupby to find the sum of all forest fires over the years. I found that there was an increasing trend.

A dashboard where the user could click on a point on the line graph which corresponds to a specific year and the number of forest fires would filter the map of Brazil to the corresponding year and show the average number of forest fires in each state would be pretty nice. So, I did that.

Monthly Trends in Forest Fires

Before I show the Tableau dashboard, I would like to show a graph which represents the monthly trend of forest fires over the years. As you can see, the graph below shows that the number of forest fires are low in the beginning of the year, increases quickly in June, peaks at July, drops a bit in September, then spikes again in October.

Looking at a bit more granular of a level, you can see the shift in the lines upward since 1998 of the number of forest fires over months. This supports the positive trend seen in the number of forest fires over the years.

An Increasing Trend of Forest Fires in Brazil

Lastly, I would like to present the Tableau dashboard I created with a short video. You can see the change in the sizes and shade of the circles that represents the average number of forest fires in each state over time. The trend line of the total number of forest fires each year is also there. Sao Paulo always has a very large average number of forest fires each year.

Once Upon A Time- NLP on Disney Movie Scripts & Their Original Stories

Introduction

Practically everyone knows some Disney movies, but not everyone knows about their original stories. The movies' original stories come from many places. For example, The Little Mermaid comes from a short story by Christian Andersen and The Hunchback of Notre Dame comes from a gothic novel written by Victor Hugo. It would be interesting to see the parallels between the Disney movie scripts and their original writings, which is exactly what my project seeks to do. In addition to finding interesting relationships between main characters in the movie scripts and original stories, my project also culminates in a rudimentary flask app that is also a book/movie recommendation system.

Methodology

I first gathered 17 Disney movie scripts and their corresponding original stories. Then, I tokenized my data in two different ways-- on the word level and on the sentence level. I tokenized my data on the word level with TF-IDF, removed punctuation and used stop-words, lemmatization, and parts of speech tagging to only keep nouns and adjectives. I did this pre-processing in order to feed my data into an NMF model to do topic modeling and also used Word2Vec and PCA to find relationships between main characters in the original stories and in the movie scripts. I also tokenized my data on the sentence/line level, keeping punctuation in order to do sentiment analysis with Vader and applied dynamic time warping techniques to compare sentiment change over time in the books and movies. With my NMF model and sentiment analysis, I was able to come up with a rudimentary book/movie recommendation system. The user puts in a story/movie from the list of 34 stories/movies they liked, a sentiment similarity weight and a topic similarity weight and the system returns a book or a movie that matches the criteria. 

My methodology is summed up in this picture:

Findings

Word2Vec & PCA

Using Word2Vec and reducing dimensions to 2 with PCA, I was able to visualize the spread of main characters in the stories and in the movies. In the original stories, there is a greater spread of main characters, with some characters closer to the words "love" and "happy" and some characters rather far away from them. However, in the movies, the main characters are bunched together and everyone seems to be relatively close to the words "love" and "happy". Does this mean that the Disney movies are just more similar to each other and sugar-coats the original stories? This idea makes sense since a lot of the original stories are more dark and does not always have happy endings. For example, Victor Hugo's novel of the hunchback of Notre Dame has a lot of the main characters dying, but the Disney version is a lot happier. 

Sentiment Analysis 

Using Vader, I was able to assign a sentiment score to each line or sentence of the movie script or story. This created a time series of sentiment change over the plot of the movie or story. I then used dynamic time warping techniques to compare sentiment change over time to compare how similar the movie and their corresponding story 'feels'. My findings show that the most similar book and movie pair is Winnie the Pooh by A.A. Milne and  The Adventures of Winnie the Pooh. The Winnie the Pooh book/movie pair received a dynamic time warping distance of 7, the lowest of all the other pairs of books and movies.  The most dissimilar book and movie according to sentiment is The Hunchback of Notre Dame by Victor Hugo and The Hunchback of Notre Dame.  This book/movie pair received a dynamic time warping distance of 33. You can see the change in sentiment over time in the following graphs. (I used a rolling mean of 5% of the lines/sentences to smooth out the graphs.)

Recommendation System

Finally, my recommendation system was created by doing topic modeling over the 34 total number of books and movies and dynamic time warping scores. NMF was able to create 34 topics that corresponded to the movie or a book very well. I also wanted to be able to create a recommendation based on how similar the user wanted the recommended book or movie to feel to their chosen book or movie and how similar in topic the user wanted the recommended book or movie to be to their chosen book or movie. To give users those options, I used cosine similarity to compare each book or movie against another book or movie using the topic weights vectors I received from NMF. I also used the dynamic time warping distances to compare how similar each book/movie was to another book/movie. 

Here is a demonstration of the flask app I built:

I will end with a quote: 

"Begin at the beginning," the King said, very gravely, "and go on till you come to the end: then stop."

-Lewis Caroll, Alice in Wonderland

Suicidal Children in the Western Pacific

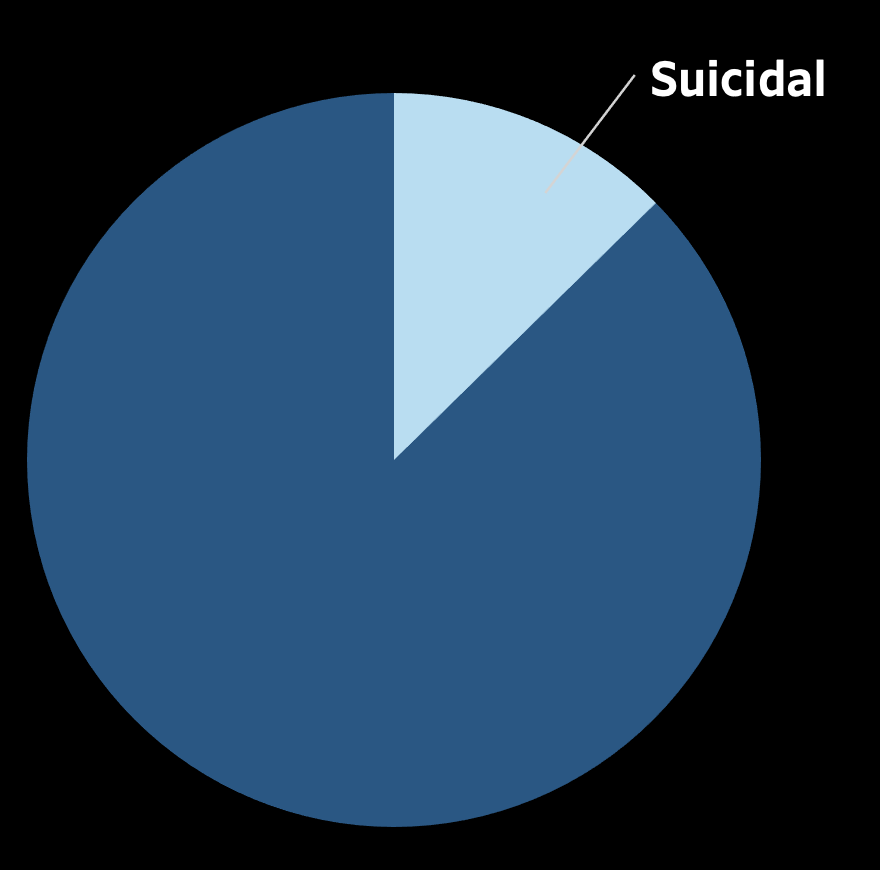
Which children are suicidal in the Western Pacific?

Why is this question important? According to a 2014 article, suicide rates in the Pacific Islands are some of the highest in the world. In countries like Samoa, Guam, and Micronesia, suicide rates are double the global average with youth rates even higher. 

I decided to look at the World Health Organization's Global School Based Health Survey taken in the Western Pacific countries, most of them in the 2010s (China's was taken in 2003). The purpose in looking at those surveys is to see if I can predict whether a child would be suicidal or not.

There is a question in the survey that asks if a child has seriously considered attempting suicide in the past 12 months in the survey. In most surveys, there are two related questions which I did not keep as my features (they would highly bias what I am trying to predict). But, I used all the other survey questions to see if I could classify whether a child has seriously considered attempting suicide or not.

In addition to the survey, I gathered information about the country itself, such as GDP and population. I combined my data tables using some SQL. 

(I used Tableau to create all of the charts I will be showing.)

According to the survey data, about 13% of children are suicidal in the surveyed Western Pacific countries.

This imbalance caused me to change my class-weights in my logistic regression model. It was a 5:1 class weight situation, where the suicidal class weighed 5 times as much as the non-suicidal class.

I used an F1 metric, weighing both precision and recall equally to evaluate my model. I received an F1 score of .42 on a hold out set using logistic regression.

I later decided to use XGBoost to potentially improve my F1 score. I did not use class weights, but did decrease the threshold for my positive class to .19 and received an F1 score of .44. 

Actually, recall is slightly higher when using logistic regression than XGBoost. I should have chosen logistic regression as my main model, or should have used an F-beta metric to weigh recall more (since it is better to catch all of the suicidal kids even though some may not really be suicidal than to not catch all of the at-risk kids). But, I chose XGBoost as my main model and looked at the feature importance. 

I found some very interesting correlations. One top feature in both my XGBoost model and one that gave a lot of signal in my logistic regression model is the loneliness factor and insomnia factor. 

Suicidal Children are 3x as Likely to Have Experienced Extreme or Moderate Loneliness

Suicidal Children are 3x as Likely to Have Lost Sleep over Excessive Worrying

Suicidal Children are 3x as Likely to Have Been Bullied

Suicidal Children are More Likely to Have Tried Cigarettes and at a Younger Age

Where are these suicidal children located?

It turns out the top three countries with the highest percentage of suicidal children (according to the survey) is in islands. 

Is it a coincidence that Samoa is in the top 3 high risk countries? I'm not too surprised, since there is an article that mentions Samoa having very high youth suicide rates. 

But, why the islands?

The article mentions that lack of economic opportunity among the youth may be the cause, but the data also paints a slightly different angle of the phenomena.

So, the takeaways:

Top conditions that are related to children to become suicidal are loneliness, bullying, worrying and insomnia and perhaps cigarette use.

Other considerations may be the child's gender and the perception on how much their parents understand their problems. Also, population and a country's colonial history shows up as important features somehow.

At the end of the day, it is hard to predict whether a child is suicidal or not from just health survey data, but it does show some interesting trends.

Go-Fund-Me

Introduction

Some of you know about GoFundMe, which is a free online fundraising platform.
With crowdfunding, people can harness social media to fund for anything from
medical expenses to honeymoon trips.

If you were a potential user of GoFundMe, it would be nice to know about how
much of your goal you would successfully be able to raise. If you know
beforehand your success rate, you will have an idea of whether or not GoFundMe
is the right place for you to raise money. I predict that what you are fundraising
for, your goal amount, and what your story is will be able to give some idea
of what percent of your goal you will be able to fundraise.

To see how predictive the category of your campaign, the goal amount and the
story is in the amount you will be able to fundraise, I decided to create a linear
regression model with those features.

Web Scraping

I did web scraping using beautiful soup and selenium to develop my database.
I then did some preprocessing, which included changing the format of my data to
extract the numbers that will be used in future analysis. Then, I did data analysis
which included locating and removing outliers and plotting residual plots. Looking
at residual plots pointed me to do some feature engineering where I used
polynomial features and one hot encoding on categories of campaigns. Lastly, I
fit models to my data by doing train-test-split and cross validation to decide which
model gave the most predictive power.

I scraped the location, story, date, category, money raised, goal, and social media
shares. Only the money raised, goal, story, and category ended up being used as
my raw features because the nature of the problem means that I start at time 0 and
have 0 social media shares. Location was removed from my features because most
of the campaigns were in the United States and I didn’t feel it was as important.
With the story, I engineered three features- word count, polarity score, and
subjectivity score. 

Data Analysis

After preprocessing the data, I was able to create some charts. I see that the
distribution of my target, the percent of goal fundraised, is left skewed. It shows that
many people do reach their fundraising goal.

The next step is to locate and remove outliers. Looking at the amount of goal, we
see that most people’s goal is to fundraise $500,000 or less. I will remove the data
points that have a goal greater than $500,000. Looking at the word count, we see
that most people have stories that are 1500 words or less, so I will remove data points
that have a word count greater than 1500.

Looking at the residual plot where I compared the features of goal amount, word
count, polarity score and subjectivity score, I see that I am either over-predicting or
under-predicting my percent of goal raised all the time. Maybe this means that using
polynomial features might help.

Modeling

Linear regression on 941 observations and using polynomial transformations of goal
amount, word count, polarity score, and subjectivity score, I received an R^2 score of .20.

Linear regression on the one-hot-encoding of categories gave me an R^2 score of -.03.

Combining the one-hot-encoding of categories and the polynomial transformations of
the four features above, I received an R^2 score of .42, which is not entirely bad
considering that I am trying to predict human behavior.

Using cross validation, I was able to see that lasso regularization gave me the 
highest R^2 score. 

Interpretation

Looking at the coefficients, I was able to see what the percent boost or reduction of
your goal by category was. The values assume that you are holding everything else
constant. 

Campaigns that get on average the highest reduction in their percent of goal
include newlywed, business, and competition categories. Campaigns that get on
average the highest boost in their percent of goal include medical, emergency, and
memorial categories.

It turns out that in addition to animals, community, creative, and event having coefficients
of 0. Polarity score, subjectivity score and their polarity score times subjectivity score also
has a coefficient of 0 under lasso regularization.  This makes sense, from our previous
F-statistic analysis, which shows that polarity might not have anything to do with percent
of goal raised.

Further Tuning of Model

One glaring error in my model is that it assumes that campaigns are completed by the
time I scraped the data. That is not true, so adding the time component into my model
will greatly fine tune my model. The question of how much one might be able to
fundraise is also a bit flawed. A better question would be how much one would expect to
be able to fundraise in a given time.

I can group my data into different bins according to a "days active" feature and do
further analysis with that. I suspect a similar trend in the categories that get a percent
boost or percent reduction in their goal will remain, but the newer model may have more
accurate predictions.

The effect of sea-level rise on Great Britain

Original Map of Great Britain

A rise in sea level of 10 meters

A rise in sea level of 50 meters

A rise in sea level of 100 meters

The graphics shown show a picture of Great Britain and the effect of sea level rising 10 meters, 50 meters, and 100 meters. The black mass represents the ocean and the lighter parts represent the land mass. You can see the white parts diminishing as sea level rises. 

I got the data from Christian Hill's online book in Chapter 7 on matplotlib.

The graphics was created from an .npy file which had arrays of the altitudes of 10 km x 10 km hectad squares of Great Britain. 

I was told to use imshow to plot the map given in the .npy file and plot the three different maps where sea level rises 10m, 50m and 100m. I also had to figure out the percentage of land area remaining, relative to its present value. 

.imshow

I used .imshow to plot the map after I opened the npy file with numpy's load function. 

The code looks like this:

plt.imshow(a, interpolation='nearest', cmap='gray')

plt.show()

where plt represents matplotlib.pyplot. Interpolation= 'nearest' was supposed to make the map more clear, but I don't think it did anything. cmap='gray' might be for the color scale.

Manipulating the arrays

To find the altitudes of the land mass when there is a sea level rise of 10m, I subtracted every element in my array by 10. This was done by just calling the given array a and subtracting 10. Since some values became negative, I had to replace all negative values by 0. That was done by the following code: 

z[z<0] = 0

where z is an array. The above code is basically saying, for all negative values in the array z, let them equal 0.

Deducing percentage of land remaining

The next step was the deduce the percentage of land mass remaining after a rise in sea level of 10m, 50m, or 100m.

Since the numpy arrays gives the average altitudes per 100km^2 of area of Great Britain, we know that we can find the total area of the map by counting the total number of elements in the arrays. There are 8118 hectad squares whose area is 811800 km^2. That counts the area of the oceans too. To just find the land mass area, we need to subtract the hectads that have an average altitude of 0. 

To count how many hectads had altitude 0, I used a for loop like so:

counter = 0

for element in a:

    for element in element:

        if element == 0:

            counter += 1

print(counter)

where a is an array.

In the original map, there were 5261 hectads with altitude 0. I subtracted the number of hectads with altitude 0 from the original number of hectads (8118) to get the number of hectads of land mass. I got that the land mass of the original map is 285700 km^2. 

I used a similar for loop to find the number of hectads of land mass with altitude greater than 0 for the latter 3 maps. Then, I compared the number with the original map's land mass. 

When sea level rises to 10m, the percentage of land remaining compared to the original land is 83.86%.

When sea level rises to 50m, the percentage of land remaining compared to the original land is 64.02%.

When sea level rises to 100m, the percentage of land remaining compared to the original land is 45.15%. 

Does it look like that in the maps?

Final Thoughts

I am very happy to know how to load some type of image through python. Although I did not create the code for the map, I have a bit of knowledge of how pictures can be created through arrays! That is very cool. I always wondered how pictures of maps were created through code, and now I know, kind of.

Climate change is also something I am very interested about. I hope to do my final project at Metis related to climate change. 

On a side note, I will be attending the Spring cohort's career day today to see them present their final projects. I am excited about that. 

Github code - Sea Level

BMI variation with GDP

How does per capita GDP compare to the BMI of men across the world? That is a question in Christian Hill's book in Chapter 7. I was asked to create a scatter plot (bonus if it was colored) to compare BMI and GDP. The size of the bubbles are relative to the population of the countries and the countries are color-coded by continent.

Reading tsv files with pandas

The 4 data sets were in tsv format, so I used pandas read_csv to read them. Each of the three data sets had a list of countries and either their population, average BMI for men, GDP per capita, or the continents the countries were in. The data sets did not have the same amount of data. Some were missing countries, some were missing values for BMI , GDP, or population.

Making Dictionaries

Since I did not know how to directly create a scatterplot from data sets that did not have an equal amount of rows, I thought I should create a dictionary that had keys as countries that have existing data on average BMI , GDP , and population to values of BMI, GDP, and population.

How can I do that?

I first made 4 dictionaries that had keys as the countries and values as either BMI, GDP, population, or continent. I first had four list of lists I had to flatten to form into four different dictionaries. I wrote a function to create a dictionary from a dataframe object.

This did not get rid of my missing values, but they will be dealt with later.

For loop

I then decided to write a for loop where for each country in my GDP dictionary, if that country is in the set of countries in my BMI dictionary (ignoring the missing countries here), then I would append a tuple that consisted of the average BMI in that country and the GDP of that country to an empty list. I later added in more elements into my tuple where the population of that country and the continent of that country was returned. (The population element was divided by 8000000 because the size of the bubbles were too large, so I had to scale the population down.)

Getting the above paragraph into code form required a lot of logical reasoning and some knowledge of how dictionaries worked!

The result is a list of tuples.

List of tuples to scatterplot

The next step was to create a scatterplot from my list of tuples. I looked it up and there is a quick way to do that. My list of tuples was named list_of_bmi_gdp and I applied

x,y,z,q= zip(*list_of_bmi_gdp)

zip combined with * will unzip a list, and the unzipped lists are assigned to x, y, z, and q.

Then, I plotted my scatter plot with the following code:

plt.scatter(x,y,s=z, c=q)

x represents my BMI (shown on my x-axis), y represents my GDP (shown on my y-axis), s = z means that my third dimension, size, will be represented by my list of population z, and c =q means that my fourth dimension, color, will be represented by my list of colors q.

Note that I had to first convert my continents into colors before I could assign c to q. That was done with a for loop like so:

for country, continent in color_dictionary.items():
    if continent == 'Europe':
        color_dictionary[country] = 'red'

matplotlib.patches


The last step is to add a legend to my scatterplot to show which colors represented what continent. I used patches to add a custom legend. I imported matplotlib.patches and mpatches.

To make a red patch, I used this code:

red_patch = mpatches.Patch(color='red', label='Europe')

To add that to my legend, I used this code:

plt.legend(handles=[red_patch, orange_patch, yellow_patch, green_patch, blue_patch, purple_patch])

About the Scatterplot

From the scatterplot, we see that Asia has several countries that have a huge population, denoted by the large orange bubbles relative to the other bubbles. However, Africa and Asia has low GDP and low BMI. There seems to be a trend where countries with higher GDP has higher BMI on average.
But, you can still see some Asian countries having relatively high GDP, but low BMI (the orange dots that are in the middle of the graph). North America seems to have the highest BMI, but also relatively high GDP. Europe is clustered at a relatively high BMI and high GDP.

Final Thoughts

I get really excited when I am asked to create multi-dimensional scatter plots because I know the results will be very nice looking. Just look at the scatter plot! It tells so much and there are so many layers too it, but not too much to be overwhelming. I had to explain to my friend what was going on, but once she got the hang of reading it, there are correlations that come up from the plot that are worthwhile to note.

I learned about patches and adding color to scatterplots in this exercise. I also learned more about the zip function and how to pull things from dictionaries.

Overall, another worthwhile problem!

Here is the code I used on Github- BMI.py